昔むかし2000年前にギリシャのツェノンという人が変な事をいいはじめました。 「アキルレウスは亀に追いつけない」というのです。 アキルレウスは古代ギリシャの強い大将で、走るのが抜群に速かったといわれています。 そのアキルレウスが亀に追いつけないというのです。
ツェノンはいいます。
「今アキルレウスが亀のいるところまで走ったとしよう。 すると亀は少し前にいる。」
「またアキルレウスが亀のいるところまで走ったとしよう。 するとまた亀は少し前にいる。」「またアキルレウスが亀のいるところまで走ったとしよう。 するとまた亀は少し前にいる。」
「だから、いつまでも、亀はアキルレウスより前にいるはずだ」というのです。
でも実際に走れば、アキルレウスはすぐ亀に追いつくに違いありません。ツェノンの理屈はどこが間違っているのでしょうか。
これに答えるには、次の数学問題の答えがわかっていなければなりません。
「ここにヘンな木があります。 今の高さは1mですが、来年は50cmのびるはずです。 その次の年はそのまた半分の25cm、その次の年はそのまた半分のびます。 その木が100年たったら、何m位になるでしょうか。
ア 100m イ 10m ウ 5m エ 2m」
では考えて下さい。」
答えは2mです。 みなさんできましたか。
 要するに1+1/2+1/4+1/8+…を計算すれば良い。
要するに1+1/2+1/4+1/8+…を計算すれば良い。やりかたはいろいろありますが、三角の面積で考えると中学生にはわかりやすい。
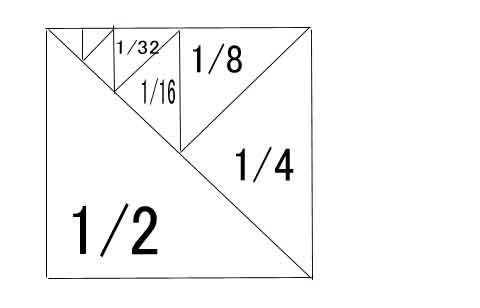
面積1平方メートルの正方形を考えましょう。 その半分の三角の面積は1/2平方メートルです。 その半分の三角の面積は1/4平方メートルです。
その半分は1/8、またその半分は1/16・・・・
図のようにいくら三角を足しても合計は1平方メートル以下です。ですから、木は100年あとだろうが、1万年あとだろうが2m以下です。
「無限に(どこまでも永久に)成長しても、実際にはあるところで止まってしまう」 「無限に(どこまでも)足しても、実際にはある数以上にはならない」
事があるのです。
アキルレウスと亀の話も、この例なのです。
今アキルレウスが亀の10倍の速さとしましょう。
亀は1キロメートル先にいるとします。 1000m
アキルレウスが1キロ走ると亀は100m先にいる。 100m
アキルレウスがまた100m走ると亀は10m先にいる。 10m
アキルレウスがまた10m走ると亀は1m先にいる。 1m
1000m+100m+10m+1m…は1111.1111…メートル …・
で、1112m以下です。 ですからツェノンの話はそれ、つまり合計1111.11…m以下の話なのです。 いくら「アキルレウスが…」という話をしても、その話を1万回繰り返しても、1111.11…mより近いところでの話で、それより先の話はカットされている。 全部の話のように見えて、実際には1111.11…mより前の話しかしていない
のです。
たしかに1111.11…mで追いつく前の話なら、いつでも亀のほうが前にいる。 それより先の話をすれば、アキルレウスのほうが前なのです。
「いつまでも増えるけれど、実際の増える程度は大したことなし」という例は実際の社会でごく普通です。 その事がわかっていないと、「いつまでも増える」…はイコール「どこまでも大きくなる」だと思い違いをして大損をする事があるのです。