これは、補教でなく、授業クラブで実施しました。
授業クラブ/選択授業では、当時技術室にあったコンピューターNEC9800を用いて、一番やさしいプログラム言語であるBASICを教え、最後がゲーム「モグラタタキ」の原理・製作とこの曲線に囲まれた面積。 曲線は放物線と円です。
残念ながら仮説実験授業ほど合理的なものにならず、大変拙い授業になりましたが…・ 生徒のやる誤りが多種多様で、誤りの種類を予想して授業をする事ができていない。 つまりお話にあたる部分=教え込む部分が不合理で生徒の誤りを少数の種類に絞る事ができないのです。
求める方法は、
1 曲線で囲まれた面の中の細かい方眼紙の正方形の数を計算機に数えさせ、その数と正方形面積の積という原始的方法で、Y=Xの二乗、X=1、Y=0 に囲まれた面積を計算する。 (計算機だから実用的時間で答が出、0.33になる)
2 積分のなり損ないのような方法で、キレイな数値(つまり1/3)が出て当然である事を示す
というものです。
現在Ｎ88ＢＡＳＩＣを使う人はいないと思うので、プログラムそのものは省略し、その骨子だけを書きます。
最初はfor X=0.1 to 1 step 0.1 （0から1まで10分割）とし、 for Ｙ=0.1 to 1 step 0.1とした上で、Ｘの自乗との大小を調べて、0.01という方眼紙1区画面積の数を1つづつ足すという原始的方法です。
次にfor X=0.05 to 1 step 0.05 とし、面積0.0025という方眼紙を数える。
その次になってやっと for X=Ａ to 1 step Ａ とし、Ａの自乗という面積の正方形の数を数える。A は1の整数分の1で、0.1、0.05,0.01、0.005と代入させる。当時の計算機ではそのあたりが限界で、それ以上細かいところまで計算
すると要する時間が実用的でない。
プログラムで数え方を変えると半分に近い時間で数えられますが、生徒にわかりにくい方法は除外とします。
はじめから細かい正方形の一辺をＡとせず、具体的数字からはじめています。
「数あてゲーム」から「簡易モグラタタキゲームとその諸欠点つぶし」までという授業をしているので、大多数生徒がこの程度のプログラムは理解できますが、代数は苦手という生徒が多いからです。
まず具体的数字で計算になれてから、それを文字に置き換えるという方法だと、式の理解困難という生徒が少なくなる。
どうも1/3に近くなったようです。 では正確に1/3なのでしょうか
正方形を小さくすればだんだん正確になりますが、計算に時間がかかりすぎます。
ではもっと正確な方法で計算をしましょう。
。それには図形を多数のの柱(長方形)に分解し、その面積を計算して寄せ集める、いう方法を使います。 さっきの方法と似ていますが、今度は0.1とか0.01という数でなく、無限に細かくした面積を計算して正確な値を出します。
図１
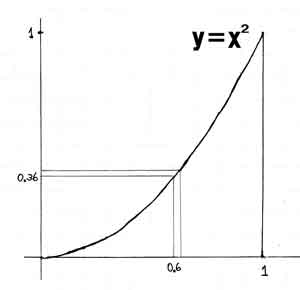
いま左の図で横xが0.6のところで0.001の幅の柱(長方形)の面積を計算しましょう。 Xが0.6ならYは二乗ですから0.36です。 柱の高さが0.36で幅0.01なら面積は0.0036です。 ただし右端Ｘ＝0.601のほうで計算すれば少し大きくなり柱の高さが0. 361201ですから、面積は0.000361201となります。
そのとき幅を狭くすれば、右の高さと左の高さの違いはほとんどなくなる事に注意しましょう。 幅が無限に狭くなればどちらで計算しても同じになる。
今度は横に長い長方形の面積を計算します。 Xが0.6のところでは横が0.6であり、縦はＹですから0.36です。 Ｘが0.601なら縦は0.361201ですから、この細く寝ている柱の面積は0.361201−0.36
=0.001201と0.6を掛けたものですから、0.0007206となります。 この面積は0.00036、0.000361201の2倍です。 幅を0.6でなく0.601で計算すれば面積は少し大きくなりますが0.000721801でやはり2倍です。
幅をもっと狭くすれば、大きいほうの数字と小さいほうの数字の違いはやはり小さくなります。
幅をどこまでも狭くしてゆけば、違いはどこまでも小さくなり、ついに同じと考えてもよくなります。 ですから0.36と0.72つまり縦長の柱の面積の2倍が横に寝た柱の面積なのです。
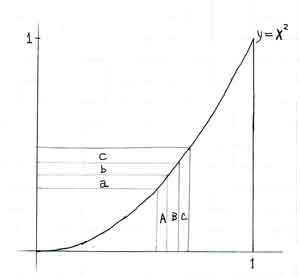
右の図を見れば、縦長の柱の面積を集めたものが放物線より下の面積であり、横に寝た柱の面積を集めたものが放物線より上でy=1までの面積です。
だから放物線より上の面積は下の面積の2倍です。
つまり下の面積は1/3であり、上の面積は2/3です。
このように図形を無限に細かく切り、またそれを寄せ集めるという計算の方法は、円の面積・円周の長さの円周率は同じという証明や、円錐体積などの公式を作るときアルキメデスが考え出しました。
この計算の方法を公式にしていろいろな図形の面積や長さの計算が簡単にできるようにしたのは、万有引力（重力）で有名なニュートンです。 積分という。
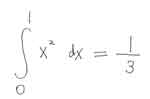高校で習いますが、今の計算を左下 のように書く。ミミズのような記号は無限に細かいものを寄せ集めるという記号で、全体とし
てはy=xの二乗というグラフを無限に細かく切り、ｘが0から1まで寄せ集め
た面積という意味です。
少し遅れてライプニッツと関孝和もそのような数学を考え出しました。
関孝和の研究はニュートンやライプニッツの研究に比べて劣る面があります が、前の二人が高校1年位だったヨーロッパの数学を高校3年位まで引き上げ たのに、関は中学1年位だった日本の数学をそこまで引き上げたのですから素 晴らしい。
日本が鎖国でなく、関がヨーロッパ一流数学者の本を読んだり一流数学者と 討論する事ができたとすれば、もっと優れた研究ができたかもしれませんね。
論理が不正確ですが、数学者以外の人間にとっては論理の正確さよりも、いろいろな論理がある事を知り、それらが直観的に使える事が大切ではないでしょうか。