土曜日が隔週休みの時代東京都西東京市立柳沢中での話です。
柳沢中では、A時間割とB時間割があり、1月から2月毎になっています。 土曜日が休みになっている授業が遅れるのを防ぐためです。
例えば理科が1週3時間になっているとして、A組は土曜に理科があり、B組C組D組は土曜に理科がないとしましょう。 そうすると
土曜に理科のあるA組は1月で授業が3+2+3+2=10時間なのに、
B組C組D組は3+3+3+3=12時間となります。
そうすると2時間の差ができるので、そのままではA組だけ実験なしとか早口でわかりにくい授業にしないと授業時間が足りない事になります。
これでは困るというので他校では、普通「つっこみ」と呼ばれる方法を使っていました。 つぶれる土曜の時間割をほかの日の午前中にやるのです。 ですから1月に2日ほど例外の時間割になっていて、1時間目と5時間目が体育になったり3時間めと5時間めが音楽になったりするクラスもありました。 先生も生徒も慣れていない臨時時間割のため、生徒は教科書や授業道具を忘れる事が多く、先生も授業の準備を忘れる事が少なくありませんでした。 また先生たちはテストまでの各クラスの時間数計算をよく間違え、2日まえになってテスト範囲が終わらないと騒ぐ先生もいました。
しかし「置換」という数学の考え方を知っていれば、そういう事はなくなります。 やさしい例で、置換の考え方を説明しましょう。
いま何かクラス対抗の学年スポーツ大会を考えましょう。 かりに種目はバレーボールかバスケットボール1種目だけとします。
クラス数が2や4なら話は簡単です。2なら1試合で終わるし、4ならトーナメントになります。 3のときは総当り3試合になるでしょう。クラス数が3や4では、試合が続いて疲れるという理由で不利なクラスもできますが、仕方ないです。クジでその損なクラスを決めることになる。
例えば3クラスでA-B B-C C-Aの順にするとAが少し有利でしょう。 4クラスで第一試合であるA-Bの勝者と第2試合であるC-Dの勝者の試合ではA-Bのほうが少し有利でしょう。
クラス数が5ならどうしたら良いでしょうか。
例えば、A-Bの試合をして、そのあと不戦勝のC、D、Eと勝ち抜きにすると、AとBは3試合に勝たないと優勝できないし、疲れも大きく大変不利になる。
次の方法はどうでしょうか。
A-B / C-D / E-A / B-C / D-E
優勝は得たセット数、セット数が同じなら得失点差で決める。
これなら、どのクラスも2試合づつで、しかも2試合連続という事がなく公平です。
特別強いクラスとあたらないクラスが2位になりやすいというなら、不戦勝をつくるトーナメントも特別強いクラスに早く当たると不利であり、同じようなものだと思いますが…。
リーグ戦にして、この5試合のほかに
A―C / B-D / C-E / D-A / E-B を足す方法なら文句はでない。ただし試合は5試合から10に増える。
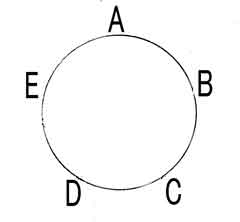
この組み合わせ方法は次のようにして作ります。
図のようにABCDEを輪の形に並べる。
最初A-Bとすれば、輪の順にCD、EA、BC、DEとなります。
最初A-Cとすれば、1つ飛んで隣との試合ですから、Bの相手はD、Cの相手はE…という風にABCDEを置き換える。Dの相手はDEAでAが1つ飛んで隣ですから、Aになる。
このように規則をきめて、字を置き換える事を数学では「置換」といいます。
では柳沢中の時間割はどうなっているのでしょう。 教室で時間割をみるだけでは体育や技術家庭が共通だという位しかわかりませんが、職員室にある大きな時間割を見ると次のようになっています。
A時間割ではK先生の数学が 2D 2A 1B
となっている場所がB時間割では2C 2B 1A
となっています。 つまりAはBに置換され、BはAに置換される。
CはDに置換され、DはCに置換されます。
そうすると、土曜の授業はA時間割とB時間割で違い、2週間ごとに潰れるクラスが違っています。 ですから特に授業数の少ないクラスはできない。
こうすると、体育や技術家庭など2クラス合同授業の場合はAB両方の時間割が同じですから、忘れ物は少なくなる。
これを数学では「柳沢中学のA時間割とB時間割が置換群になっている」といいます。
置換群というのは大学で習う数学ですが、中学でも時々応用があるのです。