圧力の話/試作品

　短いのに授業書を作る事ができず「実験つきのお話」になっています。
　本来は授業書にすべき内容ですが、いくつかの問題点があり授業書にできない。
インターネットに出す自作授業書/お話もそろそろ最後なので、なぜできないのかの理由を書いてみます。　基本的理論を教える授業書はクイズつき教材と違い、作るのが困難という実例を出す意味があるかと思います。　またどなたかが、困難を克服して下さると良いとも思います。

風船がまるくふくらむ理由
　圧力には方向がなく、圧力はどの方向にかかるというのを学びました。　それを分子で考えてみましょう。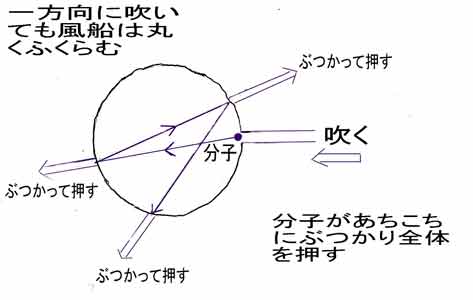



　口から飛び出した空気の分子は左にぶつかって左を押し、はねかえって右にぶつかり右を押し、またはねかえって下のほうにぶつかり、下のほうを押す・・・・これが圧力です。
　固体と違い分子が動き回ってあちこちにぶつかって押す。　だから、空気を入れた風船は丸くふくらむのです。

質問　水を風船に入れたら風船は丸くふくらむでしょうか。　
　






質問　　注射器に水を入れ、押して泡の小さくなる実験を覚えていますか？
　この時、生徒が自力で以下の絵を書けるかどうかが問題となります。　書ける生徒が1クラス数人いればこのあたりは問題にする事ができますがそのようなテストや質問をしていないので、問題にできず、お話と質問になっています。


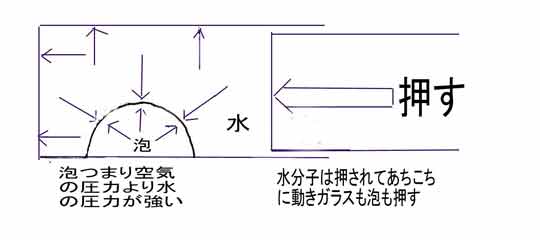
　注射器を押すと、水分子はあちことに動き回り、ガラスや泡を押すのですが、分子は弾力100％ですからどこでも同じ圧力になります。
　泡の空気の圧力は押す前と同じですから、泡は圧力の争いに負けて小さくなります。

　では注射器を引っ張るとどうなるのでしょうか。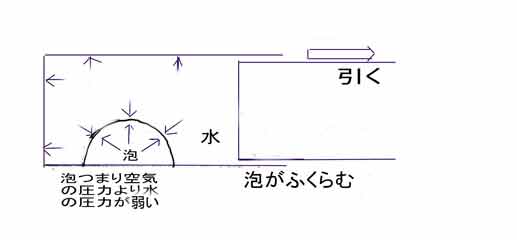　
　

　














　こちらの図だけ選択肢を出す方法も考えられます。　しかしただ書かせてどんな絵を書くかがわからないと選択肢が無意味なものになる危険があります。　一般授業形式にして黒板に案を書かせ、生徒たちと絵を完成させるというブロークン授業をすれば適切な選択肢を作る事ができるとおもわれますが、僕の現役時代にはそれをする時間的余裕がありませんでした。。
　
この図の一部文字を消して、書かせるという方法もあります。 弱いとかふくらむという単語を消すという方法です。

質問　2つの図では水の圧力があるのに書いてない面があります。　どことどこですか？
　右・・・水が注射器の中身のほうを押す圧力、と下・・・水が注射器の下のほうを押す圧力ですね。

　この質問は実際の授業にはなかった。　これを最初から書いておくと焦点がボケ図がわかりにくいという理由で、上記のような絵を描いたのだが、その結果次の段階で仮説がでにくくなっているので、苦肉の策として後から加えた（現実に授業をしていない）。

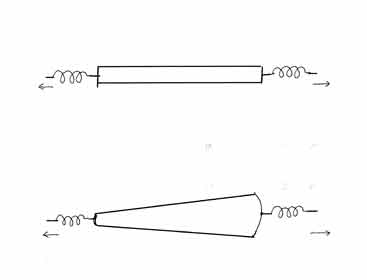質問　 図のように棒を左右から引っ張り、そのひっぱる力の大体の大きさを測るためにばねをつけましょう。
　ばねの伸び方は大体同じだと思いますか。


　質問　棒のかわりにスリコギを使います。　引っ張ったとき、ばねの伸び方は大体同じですか。

　










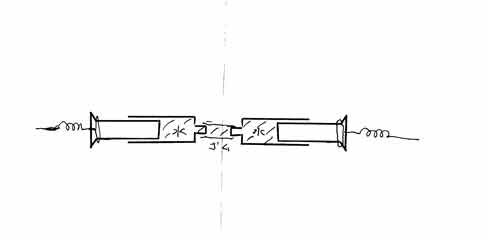　質問　　では水を入れた注射器2本を図のようにつないで測ります。　ばねの伸び方は大体同じでしょうか。

　











問題　　今度は太さの違う注射器を使います。右の注射器の太さ(断面積)は左の注射器の太さの約　　　倍です。
　引っ張ったとき、ばねの伸び方は大体同じになるでしょうか。

　









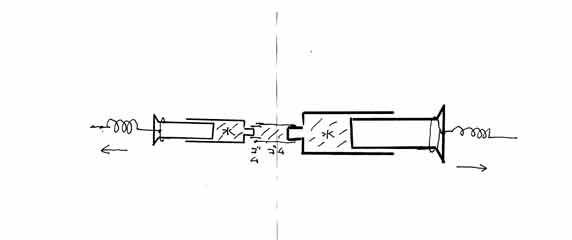
　水から注射器にかかる圧力についての前記質問があれば、ここで正しい仮説が確実に出る・・・というなら、授業書として合格だがどうだろうか。

　正しい仮説がでないクラスがあるなら、仮説が出るようにヒントの質問を増やすか、「前年の授業では・・・と援け舟を出す事になる。　要するに太いほうは圧力の矢印が増えるから、力は大きいはずという事にどれだけの生徒が気づくかは、テスト授業をしなければわからない。

　「液体や気体の圧力には方向がない」…　分子が動き回るので、圧力は全体にかかり、一方向から押したり引っ張ったりしても、全体から押したり引っ張ったりするのと同じになります。
　一番下の図では、どの注射器にも同じ圧力がかかるので断面積2倍ならその面積全体に圧力がかかって力は2倍になるのです。

　では右側の注射器にたいへん太いものを使ったら、2本のばねの伸び方がどうなるかわかりますね。

　　では今度は風がふいている時、縦にしたボール紙を風の方向と垂直に持ったとしましょう。　ボール紙にまともに風があたり、ボール紙が動かないように支えるには力が要ります。

　ボール紙を2枚にすると風から受ける力は何倍になりますか。
　ボール紙の面積を2倍にすると風から受ける力は何倍ですか。
　ボール紙の面積が3倍なら?

　風の場合も、水の場合も面積が2倍、3倍になると力は2倍.3倍になります。
　
　「圧力が同じでも、面積が2倍、3倍になると力は2倍、3倍になる」のです。
また風の圧力が2倍.3倍でも、受ける力は2倍、3倍です。

　このあたりは強引な感じである。　もう少しスマートに押し付ける方法がないだろうか。

　これらを式で書けば、　定数×面積イコール　力　　圧力が一定の場合
　　　　　　　　　　　　　　　定数×圧力イコール　力　　面積が一定の場合
　　　　　　　　　　　　　　　
　つまり　　　　　　　　　　圧力が定数×面積　　　　　イコール　力　　
　　　　　　　　　　　　　　　圧力　　　　×面積が定数　イコール　力　　
　
まとめると(　定数が1になように単位を適当に決めれば)
　　　　　　　　　　　　　　　圧力×面積　　イコール力　となります。

　　強い風のとき、傘をさしたままより、傘をすぼめたほうが楽です。風の当たる面積を小さくすれば風の力は小さくなる。
　同じ水道でも、ふつうの蛇口の水は止めるときそれほど大きな力は要りません。水圧が低いと指で止められる事がある。　ところが校庭にある大きな散水栓の水は止めようとすれば人間が吹っ飛ばされます。　水の出る圧力は同じでも面積が大きいと力も大きくなるのです。
このあと教科書を読んで計算練習。